검색결과 리스트
글
OpenCV + CUDA 직접 빌드하기 (Windows/Linux 종합)
최근에 opencv에 있는 dnn을 한번 써보려고 직접 소스를 받아서 빌드(build)해 보았다. 역시나 엄청난 삽질의 연속이고 할 때마다 이것 저것 해결책을 검색하느라 많은 시간을 소모한다 (삽질은 누구나 한다..).
그동안 opencv 빌드를 한두 번 해본 것이 아닌데도 매번 이렇다. 이게 다 앉았다 돌아서면 잊어버릴 나이인데도 기록을 잘 하지 않았기 때문이다. 이번 기회에 opencv 빌드에 필요한 내용들을 다시 한번 정리해 둔다. 먼저, windows 빌드부터 적고 linux 빌드는 끝에서 잠깐 설명한다.
1. Windows에서 OpenCV+CUDA 빌드
준비사항 (Requirements)
- opencv: https://github.com/opencv/opencv
- opencv contrib: https://github.com/opencv/opencv_contrib
- CMake: https://cmake.org/download/
- GPU: https://en.wikipedia.org/wiki/CUDA#GPUs_supported
- CUDA: https://developer.nvidia.com/cuda-toolkit-archive
- cuDNN: https://developer.nvidia.com/rdp/cudnn-archive
- VTK: https://vtk.org/download/
opencv git에는 주요 핵심 모듈들만 들어있기 때문에 opencv의 모든 기능을 사용하기 위해서는 opencv contrib도 같이 다운로드 받는다. cmake는 가급적 가장 최신 버전을 사용하는게 좋고, CUDA는 자신의 그래픽카드(GPU)를 지원하는 버전으로 다운로드 한다(https://en.wikipedia.org/wiki/CUDA#GPUs_supported에서 확인). cuDNN은 사용할 CUDA 버전에 맞는 것을 다운로드한다. VTK는 opencv의 viz 기능을 이용할 경우에만 다운로드 받는다.
CUDA와 cuDNN 설치
- CUDA는 설치 파일만 실행하면 알아서 설치된다. 단, 중간에 설치 옵션을 물어보는데 나처럼 성질이 까칠한 사람은 빠른설치(권장) 옵션이 아닌 사용자 정의 옵션을 선택할 것이다. 이 때, 다른 것은 다 제외시키더라도 development, runtime, visual studio integration는 꼭 선택해 준다. 그리고 driver도 같이 선택해 주는게 좋겠다. (다른 것들은 설치 안해도 관계없다)
- cuDNN은 설치파일이 아니고 단순 압축파일이다. 압축을 풀어서 CUDA가 설치된 폴더에 파일들만 복사해 주면 된다. cuDNN 압축을 풀면 bin, include, lib\x64 3개의 폴더가 나온다. 만일 CUDA가 설치된 폴더 위치가 CUDA_ROOT = "C:\Program Files\NVIDIA GPU Computing Toolkit\CUDA\v11.3"라 하면 bin에 있는 파일들은 CUDA_ROOT\bin 폴더에, include에 있는 파일들은 CUDA_ROOT\include 폴더에, 그리고 lib\x64에 있는 파일들은 CUDA_ROOT\lib\x64 폴더에 복사해 준다.
VTK 빌드
opencv를 빌드할 때 가장 피곤한 부분이 VTK를 빌드하는 것이다. VTK는 opencv의 viz를 사용할 때만 필요하기 때문에 viz를 사용하지 않는다면 바로 다음의 OpenCV 빌드로 넘어가면 된다. 개인적으로는 어쩔 수 없이 viz를 사용해야 하는데 opencv를 빌드할 때마다 VTK 쪽에서 문제를 일으킨다. 그리고 VTK는 빌드(컴파일+링크) 시간도 오래 걸린다. 빌드는 CMake(사용법은 https://darkpgmr.tistory.com/102 참조)로 하면 되는데, VTK 자체는 별 문제없이 빌드되지만 항상 opencv와 연결할 때 문제가 생긴다. CMake로 프로젝트를 생성할 때 BUILD_SHARED_LIBS를 제외하고 대부분 기본설정을 사용한다.
- BUILD_SHARED_LIBS = OFF (체크 해제)
opencv에 static으로 링크할 생각이므로 BUILD_SHARED_LIBS는 OFF(체크해제)로 설정한다. 만일, 이 옵션을 ON시키면 수많은(약 120개) dll 파일들이 생성되고, opencv를 사용할 때 이 dll 파일들을 항상 같이 가지고 다녀야 하는 불상사가 발생한다.
OpenCV 빌드 (main + contrib을 하나의 world 파일로)
목표는 opencv의 모든 기능(contrib 포함)을 하나의 파일(opencv_worldxxx.dll, lib)로 빌드하는 것이다. 그 방법은 비교적 간단하다.
- opencv_contrib\modules\ 밑에 있는 모든 내용을 opencv\modules\로 이동시킨다. --> 요즘은 이렇게 안해도 OPENCV_EXTRA_MODULES_PATH 만 설정하면 알아서 하나로 합쳐주는지는 잘 모르겠다..
- opencv 빌드용 폴더(e.g. opencv_build)를 하나 만들고 cmake를 이용해서 필요한 설정을 한 후 프로젝트를 생성한다.
- opencv_build\OpenCV.sln을 열어서 ALL_BUILD 프로젝트를 빌드한다.
- 마지막으로 INSTALL 프로젝트를 빌드한다 (ALL_BUILD로 생성된 include, lib, dll 파일들을 한 곳에 모아주는 역할). 이 때, build만 하고 절대로 rebuild를 하면 안된다. 자신도 모르게 전체 프로젝트를 rebuild하는 불상사가 발생할 수 있다.
cmake gui에서 빌드 설정은 개인 취향껏 하면 되지만, 중요한 것들을 정리해 보면 다음과 같다.
- BUILD_SHARED_LIBS = ON (static으로 빌드할 것이면 OFF)
- BUILD_WITH_STATIC_CRT = OFF
- BUILD_opencv_world = ON
- OPENCV_ENABLE_NONFREE = ON
- OPENCV_EXTRA_MODULES_PATH = (contrib + main을 하나로 합쳤기 때문에 필요가 없음. 공백으로 그대로 둠)
- CPU_BASELINE = AVX (https://www.intel.co.kr/content/www/kr/ko/support/articles/000005779/processors.html 참조)
- CPU_DISPATCH = (공백으로 둠)
- OPENCV_DNN_CUDA = ON
- WITH_CUDA = ON
- WITH_CUDNN = ON
- WITH_CUBLAS = ON
- WITH_CUFFT = ON
- CUDA_FAST_MATH = ON
- CUDA_ARCH_BIN = 6.1;7.5;8.6 (https://en.wikipedia.org/wiki/CUDA#GPUs_supported에서 GPU별 compute capability 숫자 참조)
기타 개인적으로 설정하는 옵션들 (나머지는 기본값 사용)
- BUILD_PACKAGE = OFF
- BUILD_PERF_TESTS = OFF
- BUILD_TESTS = OFF
- BUILD_opencv_apps = OFF
- VTK_DIR = "..." (VTK의 빌드 폴더 root)
※ CPU_BASELINE
opencv cmake 옵션들 중 CPU_BASELINE은 사용할 CPU 명령어 셋을 선택하는 것으로서 SSE1 < SSE2 < SSE3 < SSE4 < AVX < AVX2 < AVX-512 순으로 향상된(빠른) 명령어 셋을 의미한다. 명령어 셋은 컴퓨터(CPU)에서 지원을 해야만 사용 가능하기 때문에 빌드한 opencv를 여러 컴퓨터에서 사용하고자 한다면 낮은 버전(SSE4 등)을 CPU_BASELINE으로 설정하고, 자신만 사용할 것이라면 자신 컴퓨터에서 지원하는 최대 명령어 셋을 CPU_BASELINE으로 설정하면 된다. CPU 버전 별 지원 명령어 셋은 https://en.wikipedia.org/wiki/Advanced_Vector_Extensions를 참조한다 (인텔의 경우 https://www.intel.co.kr/content/www/kr/ko/support/articles/000005779/processors.html). 요즘 대부분의 PC는 AVX2까지는 지원하기 때문에 공용 빌드의 경우에는 AVX나 AVX2 정도로 설정하면 적당할 듯 싶다.
※ CUDA_ARCH_BIN
CUDA_ARCH_BIN에는 사용할 그래픽카드(GPU)의 compute capability 값을 적어준다. GPU별 compute capability 값은 https://en.wikipedia.org/wiki/CUDA#GPUs_supported를 참조한다 (예를 들어, RTX 2080은 7.5, RTX 3080은 8.6). 빌드한 opencv를 여러 컴퓨터나 GPU에서 사용할 예정이라면 지원할 GPU compute capability 값을 모두 적어주면 된다. 단, 여러 값을 적을수록 빌드 시간은 엄청나게 늘어나기 때문에 필요한 정도만 적는 것이 좋다 (지금 몇 시간째 빌드 중인데 끝날 기미가 안보인다..)
※ 참고 사항 (빌드시간 단축)
WITH_CUDA, OPENCV_DNN_CUDA을 활성화시키면 opencv 빌드시간이 정말 오래 걸린다 (몇 시간씩). 따라서, CUDA 쪽을 사용할 것이 아니면 이 옵션은 OFF시키고 빌드하는 것이 좋다. 하지만, CUDA 쪽을 사용해야만 하는 경우 빌드시간을 조금이나마 줄이기 위해 참고할 만한 내용은 다음과 같다.
- CUDA_ARCH_BIN 개수를 최소화
- visual studio에서 Tools/Options/Projects and Solutions/Build and Run/maximum number of parallel project builds 값을 자신 컴퓨터 CPU의 논리 프로세서 수로 설정 (작업관리자 - 성능 탭에서 확인 가능)
- visual studio에서 debug 버전과 release 버전을 하나씩 빌드 (Build/Batch Build... 기능을 이용해서 debug, release를 같이 빌드할 경우에는 빌드 시간이 증가하는 것으로 보임).
- 디스크 입출력 속도가 중요하므로 SSD 등에서 빌드 (내 경우는 아예 전용 파티션을 하나 생성해서 사용함)
OpenCV + VTK 문제 해결 (OpenCV 4.5.2 기준)
VTK 때문에 opencv와 vtk를 몇 번을 다시 빌드하고 지우고 했는지 모르겠다. 현재 VTK 홈페이지에서는 VTK 9.0.1, 8.2.0, 7.1.1의 3가지 버전을 다운로드 받을 수 있으며 각 버전별 문제 및 해결 방법은 다음과 같다.
[VTK 9.0.1 + OpenCV]
opencv 4.5.2의 경우 cmake 설정창에서 VTK_DIR을 VTK 빌드 폴더로 설정하고 configure를 실행하면 TARGET opencv_viz를 찾을 수 없다는 CMake Error가 발생한다(get_property could not find TARGET opencv_viz). 단, 이 에러는 BUILD_opencv_world = ON 설정시에만 나타나고, OFF시에는 발생하지 않는다. 즉, opencv_viz를 개별 dll로 빌드할 경우에는 문제가 발생하지 않는다. BUILD_opencv_world = ON을 유지하고 싶은 경우에 한 가지 해결책은 opencv_world에서 viz만 제외시키는 것이다 (viz를 제외한 다른 모든 모듈들은 opencv_world로 통합).
- 부분적 해결책: https://github.com/opencv/opencv/blob/master/cmake/OpenCVModule.cmake#L848을 아래와 같이 변경
if(BUILD_opencv_world AND OPENCV_MODULE_${the_module}_IS_PART_OF_WORLD AND NOT "${the_module}" STREQUAL "opencv_viz")
[VTK 8.2.0 + OpenCV]
opencv의 cmake 설정창에서 VTK_DIR을 VTK 빌드 폴더로 설정한 후 configure를 실행하면 "VTK is not found. Please set -DVTK_DIR in CMake to VTK build directory, or to VTK install subdirectory with VTKConfig.cmake file"라는 에러메시지와 함께 VTK 설정이 실패한다. 분명히 VTK 빌드 폴더를 제대로 지정해 주었음에도 이 에러는 계속 발생한다. cmake에서 VTK를 발견하지 못했다는 것인데, 인터넷 검색으로는 도무지 해결이 안되어서 결국 cmake 파일들의 내용을 모두 살펴보고 해결책을 찾았다.
- 해결책: opencv 소스에서 opencv/cmake/OpenCVDetectVTK.cmake파일의 L1~L15를 아래와 같이 주석처리 (단, 9.x.x 대의 VTK 버전을 사용할 경우에는 주석 처리하면 안됨)
| # VTK 9.0 #if(NOT VTK_FOUND) # find_package(VTK 9 QUIET NAMES vtk COMPONENTS # FiltersExtraction # FiltersSources # FiltersTexture # IOExport # IOGeometry # IOPLY # InteractionStyle # RenderingCore # RenderingLOD # RenderingOpenGL2 # NO_MODULE) #endif() # VTK 6.x components if(NOT VTK_FOUND) find_package(VTK QUIET COMPONENTS vtkInteractionStyle vtkRenderingLOD vtkIOPLY vtkFiltersTexture vtkRenderingFreeType vtkIOExport NO_MODULE) IF(VTK_FOUND) IF(VTK_RENDERING_BACKEND) #in vtk 7, the rendering backend is exported as a var. find_package(VTK QUIET COMPONENTS vtkRendering${VTK_RENDERING_BACKEND} vtkInteractionStyle vtkRenderingLOD vtkIOPLY vtkFiltersTexture vtkRenderingFreeType vtkIOExport vtkIOGeometry NO_MODULE) ELSE(VTK_RENDERING_BACKEND) find_package(VTK QUIET COMPONENTS vtkRenderingOpenGL vtkInteractionStyle vtkRenderingLOD vtkIOPLY vtkFiltersTexture vtkRenderingFreeType vtkIOExport NO_MODULE) ENDIF(VTK_RENDERING_BACKEND) ENDIF(VTK_FOUND) endif() |
- 원인: opencv/cmake/OpenCVDetectVTK.cmake의 내용은 먼저 VTK 9.x.x를 찾고 실패하면 하위 버전 순서로 VTK를 찾는 것인데, VTK 9.x.x에 실패하면 사용자가 설정한 VTK_DIR 환경변수가 초기화가 되어서 이후 하위 버전 탐색이 정상 실행되지 않는 것으로 추측됨
- VTK 7.1.1 버전에서도 동일한 문제가 발생하며 해결책도 동일함
2. Linux에서 OpenCV + CUDA 빌드 (한글 지원 포함)
앞서 설명한 내용들은 윈도우즈 빌드를 대상으로 하지만, 일부 내용들(cmake 설정 등)은 linux 빌드에도 동일하게 적용된다. 리눅스에서의 빌드는 shell script 형태로 간단하게 설명한다.
CUDA, cuDNN 설치
여기서는 여러 버전의 CUDA 라이브러리를 시스템에 같이 설치하는 것을 예로 한다 (필요할 때마다 버전을 바꿔가면서 사용할 수 있도록)
1. 시스템 그래픽 드라이버 설치 (최신버전으로 설치됨)
- $ sudo apt update
- $ sudo apt install cuda-drivers
- 설치후 반드시 시스템 재부팅
2. CUDA 라이브러리 설치 (e.g. 10.2, 11.3를 같이 설치하는 경우)
- $ sudo apt update
- $ sudo apt install cuda-toolkit-10-2
- $ sudo apt install cuda-toolkit-11-3
3. cuDNN 설치
먼저, CUDA 버전에 맞는 cuDNN 파일들을 다운로드한다 (https://developer.nvidia.com/rdp/cudnn-archive)
- cudnn-10.2-linux-x64-v8.2.0.53.tgz
- cudnn-11.3-linux-x64-v8.2.0.53.tgz
다음과 같은 설치 script 파일을 생성한 후 실행 (e.g. cudnn_install.sh)
- $ chmod a+x cudnn_install.sh
- $ ./cudnn_install.sh
| #cudnn_install.sh tar -xzvf cudnn-10.2-linux-x64-v8.2.0.53.tgz sudo cp cuda/include/cudnn*.h /usr/local/cuda-10.2/include sudo cp -P cuda/lib64/libcudnn* /usr/local/cuda-10.2/lib64 sudo chmod a+r /usr/local/cuda-10.2/include/cudnn*.h /usr/local/cuda-10.2/lib64/libcudnn* rm -rf cuda tar -xzvf cudnn-11.3-linux-x64-v8.2.0.53.tgz sudo cp cuda/include/cudnn*.h /usr/local/cuda-11.3/include sudo cp -P cuda/lib64/libcudnn* /usr/local/cuda-11.3/lib64 sudo chmod a+r /usr/local/cuda-11.3/include/cudnn*.h /usr/local/cuda-11.3/lib64/libcudnn* rm -rf cuda |
시스템의 default CUDA 설정 (10.2를 default로 설정할 경우)
- $ cd /usr/local
- $ sudo rm cuda
- $ sudo ln -s cuda-10.2 cuda
시스템 환경변수 등록 (CUDA 라이브러리 탐색 순서 설정)
- $ sudo vi /etc/profile.d/cuda.sh # cuda.sh 파일 생성
- 아래 내용으로 해당 파일 내용을 생성 후 저장
| export LD_LIBRARY_PATH=$LD_LIBRARY_PATH:/usr/local/cuda/lib64:/usr/local/cuda-10.2/lib64:/usr/local/cuda-11.3/lib64 |
OpenCV + CUDA 빌드
CUDA가 준비되면 이제 opencv를 빌드해 보자. Linux에서의 opencv 빌드는 shell script 파일 형식으로 설명한다. 일부 내용은 자신에 맞게 수정한다.
| # 참고한 사이트 # 1. https://linuxize.com/post/how-to-install-opencv-on-ubuntu-18-04/ # 2. https://webnautes.tistory.com/1030 # 3. https://kkokkal.tistory.com/1325 # 과거 설치된 opencv 버전이 있을 경우 제거 sudo apt purge libopencv* python-opencv sudo apt autoremove # 위험할 수 있으니 내용을 잘 확인하고 실행 (opencv 관련만 삭제하는지..) # update ubuntu system to latest sudo apt update #sudo apt upgrade # 시스템 전체를 업그레이드하는 것임 (필요한 경우만 실행) # install relevant packages (libfreetype, libharfbuzz는 opencv에서 한글지원 위해서 설치) sudo apt install build-essential cmake git pkg-config libqt4-dev \ libavcodec-dev libavformat-dev libswscale-dev libv4l-dev v4l-utils \ libxvidcore-dev libx264-dev libxine2-dev libjpeg-dev libpng-dev libtiff-dev libjasper-dev \ gfortran openexr libatlas-base-dev python3-dev python3-numpy \ libgl1-mesa-dri libqt4-opengl-dev libeigen3-dev \ libfreetype6-dev libharfbuzz-dev # 한글 지원을 위해 필요 # download opencv git clone https://github.com/opencv/opencv.git git clone https://github.com/opencv/opencv_contrib.git # cmake setup (설정은 자신이 원하는대로 수정하거나 추가, 삭제) cd ./opencv mkdir build && cd build cmake -D CMAKE_BUILD_TYPE=RELEASE \ -D CMAKE_INSTALL_PREFIX=/usr/local \ -D WITH_TBB=OFF \ -D WITH_IPP=OFF \ -D WITH_1394=OFF \ -D BUILD_WITH_DEBUG_INFO=OFF \ -D BUILD_DOCS=OFF \ -D BUILD_EXAMPLES=OFF \ -D BUILD_TESTS=OFF \ -D BUILD_PERF_TESTS=OFF \ -D WITH_CUDA=ON \ -D WITH_CUDNN=ON \ -D OPENCV_DNN_CUDA=ON \ -D CUDA_FAST_MATH=ON \ -D CUDA_ARCH_BIN=7.5 \ # 자신 GPU의 compute capability 값 -D WITH_CUBLAS=ON \ -D WITH_CUFFT=ON \ -D WITH_QT=ON \ -D WITH_GTK=OFF \ -D WITH_OPENGL=ON \ -D WITH_V4L=ON \ -D WITH_FFMPEG=ON \ -D WITH_XINE=ON \ -D BUILD_NEW_PYTHON_SUPPORT=ON \ -D INSTALL_C_EXAMPLES=OFF \ -D INSTALL_PYTHON_EXAMPLES=OFF \ -D OPENCV_GENERATE_PKGCONFIG=ON \ -D OPENCV_EXTRA_MODULES_PATH=../../opencv_contrib/modules \ -D OPENCV_ENABLE_NONFREE=ON \ -D BUILD_EXAMPLES=OFF .. # check number of cores of your system nproc # 자신 시스템의 코어 수 확인 # build (modify the core number '12' after option -j accordingly) make -j12 # 자신 시스템 코어 수에 맞게 -j 다음의 숫자를 변경 # install sudo make install # check if it is installed successfully pkg-config --modversion opencv4 |
설정값 중에서, GPU별 compute capability 값은 https://en.wikipedia.org/wiki/CUDA#GPUs_supported를 참조한다 (예를 들어, RTX 2080은 7.5, RTX 3080은 8.6).
위 내용을 shell script 파일로 만들어서 아래와 같이 실행하면 GPU 지원 opencv가 설치된다 (e.g. opencv_install.sh라는 이름으로 스크립트를 생성했을 경우). 만일 CUDA를 사용하지 않을 경우에는 설정에서 WITH_CUDA부터 WITH_CUFFT까지를 모두 삭제하거나 OFF로 바꾼다.
$ nproc # 자신의 시스템 코어 수 확인
$ nvidia-smi # 자신의 GPU 확인
$ vi opencv_install.sh # opencv_install.sh 내용 편집
--> make -j12에서 12를 자신의 시스템 코어 수로 변경
--> CUDA_ARCH_BIN 값을 자신 GPU의 compute capability 값으로 변경
--> 기타 필요한 설정 등을 변경
$ chmod a+x opencv_install.sh # 실행 가능한 파일로 변경
$ ./opencv_install.sh # 스크립트 실행
$ sudo vi /etc/ld.so.conf.d/opencv.conf # opencv conf 파일 생성
--> /usr/local/lib 라인 추가 (opencv 설치된 라이브러리 폴더를 알려주는 것)
$ sudo ldconfig -v # 생성한 opencv conf 반영
OpenCV에서 이미지에 한글 출력하기
opencv에서는 기본적으로 cv::putText로 이미지에 한글을 출력하면 글자가 깨진다. 하지만, 위와 같이 libfreetype6-dev, libharfbuzz-dev를 먼저 설치한 후에 opencv를 빌드하면 한글 출력이 가능해진다. 단, linux 빌드의 경우만 해당되며 윈도우즈에서도 한글 출력되도록 빌드해 보고자 했지만 결국 실패하였다. 어쨌든, 한글 출력 사용법 예제는 다음과 같다.
먼저, 한글 폰트를 다운로드해서 시스템에 저장한다. (e.g. test/font/)
- 한글폰트 다운로드: font_korean.zip
- test/font/gulim.ttf
- test/font/batang.ttf
예제 코드(참고사이트: https://kkokkal.tistory.com/1325):
| #include "opencv2/freetype.hpp" int main(void) { Mat src = imread("sample.bmp", IMREAD_COLOR); // FreeType2 객체 생성 cv::Ptr<cv::freetype::FreeType2> ft2 = cv::freetype::createFreeType2(); // 글꼴 불러오기 ft2->loadFontData("test/font/gulim.ttf", 0); // 문자열 출력 ft2->putText(src, u8"Hello?", Point(50, 50), 50, Scalar(255, 255, 255), -1, LINE_AA, false); ft2->putText(src, u8"안녕하세요!", Point(50, 120), 50, Scalar(0, 255, 255), -1, LINE_AA, false); imshow("src", src); waitKey(0); return 0; } |
☞ 후기
사실 이런 괜한 삽질을 한 이유는 최근 yolo 사이트를 둘러보다가 opencv dnn을 이용해서 yolo를 돌리면 속도가 크게 증가한다는 표를 봤기 때문이다(608x608 이미지의 경우 darknet은 53fps, opencv fp16은 115fps라고 나온다). 직접 빌드해서 돌려보니 내 경우는 opencv가 좀더 빠른 것은 맞지만 그 정도는 아니다 (opencv의 경우, image blob 생성 및 non-max-suppression 시간 등은 제외하고 순수 network forward 시간만 측정한 것 같다). 실제 돌려보면 이미지 입력부터 결과 출력까지 608x608 기준으로 darknet은 42 fps, opencv fp16은 54 fps 정도가 나온다. 416x416 기준으로는 darknet은 75 fps, opencv fp16도 75 fps로 동일하게 나온다. 고해상도로 갈수록 속도가 빨라지는 것 같다. 어쨌든 빨라졌으니 좋은 것이긴 한데, 문제는 opencv dnn 버전은 yolov3, yolov4로는 동작하지만 yolov4-csp 등에서는 동작하지 않는다는 점이다. 윈도우즈 버전으로 테스트한 것이기 때문에 linux에서는 결과가 다를지도 모르겠다. 참고로 fp16은 floating point 데이터 표현 및 연산을 16비트로 처리한다는 의미이다(기본은 32비트). opencv dnn을 이용한 yolo 사용은 YashasSamaga/main.cpp를 참고한다.
| darknet yolo | opencv dnn fp16 |
| 다양한 yolo 버전을 모두 지원(yolo, yolo-csp, yolo-mesh 등) 별도로 darknet을 빌드해서 사용해야 함 |
yolov3, ylov4 등 기본 버전만 지원 darknet 빌드 없이 opencv 자체에서 yolo 수행 dnn빌드로 opencv dll 파일의 크기가 커짐 (428MB) 속도가 조금 더 빠름 (정확도는 darknet yolo와 동일) |
by 다크 프로그래머
'프로그래밍' 카테고리의 다른 글
| Matlab 핸드북 (참고용) (0) | 2017.11.21 |
|---|---|
| 프로그래밍 공부 방법 (16) | 2014.07.31 |
설정
트랙백
댓글
글
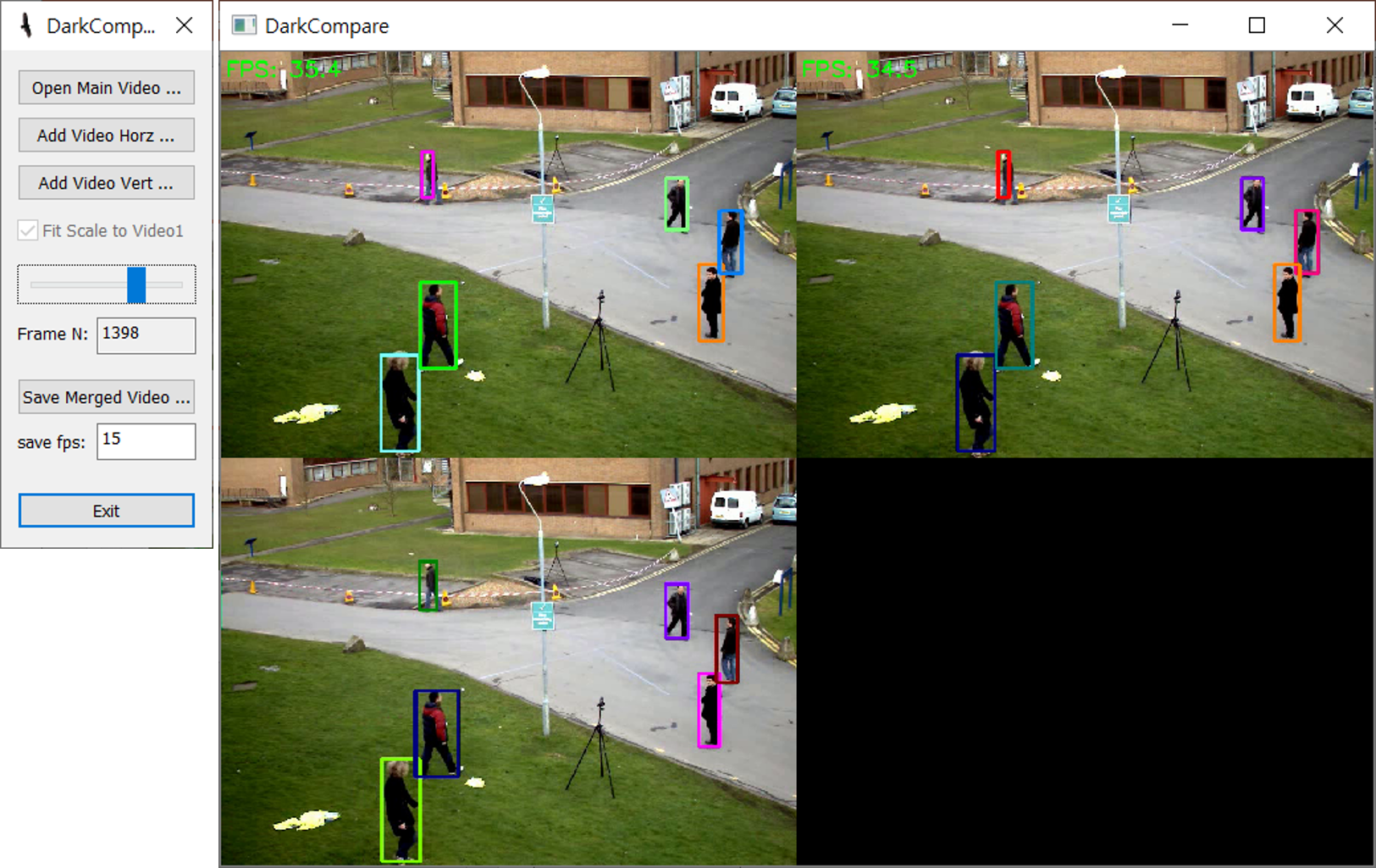
DarkCompare - 동영상 비교/병합 프로그램
동영상 여러 개를 (원하는데로) 상하좌우로 붙여가면서 비교할 수 있는 간단한 프로그램입니다.
알고리즘별 결과를 프레임별로 비교하기 위해서 만든 툴인데, 필요한 분은 사용하시기 바랍니다. 동영상 비교 뿐만 아니라 동영상들을 하나로 합치는 용도로도 사용할 수 있습니다.
- 화살표키/PgUp/PgDn/Home/End로 프레임 이동 (delay 없이 빠른 이동 가능)
- 무설치 실행
- 윈도우즈 전용
다운로드(실행파일): darkcompare1.0.zip
by 다크 프로그래머
'개발한 것들' 카테고리의 다른 글
| 테트리스 (Tetris) (8) | 2020.10.18 |
|---|---|
| DarkLabel - 비디오/이미지 객체 레이블링 툴 (Video/Image Labeling and Annotation Tool) (194) | 2017.07.18 |
| 카메라 캘리브레이션 프로그램 (DarkCamCalibrator) (169) | 2014.07.17 |
설정
트랙백
댓글
글
글쓰기에 대해
이 글은 그 동안 글쓰기에 대해 생각한 것들, 도움이 될 만한 것들을 정리한 글입니다.
자신의 글
가장 기본적인 것이지만 자신이 소화한 내용, 자신의 생각과 이해를 바탕으로 해야 진정한 자신의 글이라 할 수 있다. 조금 부족하더라도 비록 남들처럼 멋지진 않더라도 자신의 내용으로 글을 쓰자.
자신의 글이지만 남에게 보여주는 글
글을 쓰는 사람은 자신이지만, 글을 읽을 사람은 타인임에 유의하자. 타인의 입장에서 모호함이 없게, 타인이 이해하기 쉽게 글을 써야 한다. 글은 나의 지식과 나의 이해를 바탕으로 한다. 그래서 보통 자신이 쓴 글을 자신이 읽을 때에는 글에 비약이나 모호한 표현, 부족한 부분이 있더라도 읽는데 큰 어려움이 없다. 그 이유는 글을 있는 그대로 읽지 않고 우리의 뇌가 일종의 착시현상처럼 글을 쓸 당시의 생각으로 메꿔서(바꿔서) 읽기 때문이다. 그런데, 타인은 나와 지식과 경험을 공유하지 않기에 자신처럼 글을 읽거나 이해할 수 없다. 자신이 쓴 글을 한달 쯤 지난 후에 다시 읽어보자. 만일 그 때도 술술 읽혀진다면 그 글은 타인의 입장에서도 잘 쓰여진 글이다.
자기소개서
'자신의 글이지만 남에게 보여주는 글'의 결정체가 바로 자기소개서가 아닌가 싶다. 자기소개서는 자신의 얘기이다 보니 감정이 들어가고 다소 장황한 글이 되기 쉽다. 그런데, 읽는 사람 입장에서는 이러한 글이 부담스러울 수 있다. 자기소개서의 목적은 이 사람이 업무에 적합한 사람인가를 판단하기 위함이기에 목적에 맞게 글을 정리하면 좋겠다. 내용적으로는 자신에게 의미있는 것들 중에서 보여주고 싶은 것, 그리고 상대방이 관심있어 할 만한 것 위주로 구성하면 좋을 것 같다 ('내가 그 사람 입장이라면 무엇을 볼 것인가?'). 그리고 형식적으로는 길게 이어지는 서술형보다는 글을 단락으로 나누고 각 단락의 앞에 짧은 소제목(굵은 폰트로 강조)을 붙이면 효과적이다. 바쁜 현대에서 소제목만 보고도 대략적인 내용을 알 수 있다면 보다 효과적으로 자신을 전달할 수 있다. 그리고 소제목이 인상적이라면 세부 내용도 관심을 가지고 읽어볼 수 있다.
발표자료
발표자료를 준비하는 것도 일종의 글쓰기와 같다. 내 발표를 들을 사람과 내가 발표(전달)할 내용을 고려한 글쓰기이다. 개인적으로 싫어하는 발표자료는 페이지 안에 모든 내용이 빡빡하게 채워진 자료이다. 그런 자료는 발표자의 시각이 없는 자료로서 눈에 잘 들어오지도 않고 읽기도 어렵다. 발표자료는 모든 내용(지식)보다는 자신이 발표하고 싶은 내용을 보여주는 것이 기본이다. 자료의 페이지 하나, 그림 하나에도 전달하고 싶은 메시지가 있어야 한다 (발표하지 않을 세부 내용들은 별첨 자료로 빼도 좋다). 그리고, 발표자료도 또한 남에게 보여주기 위한 것이니 보는 사람이 이해하기 쉽도록 작성하는 것이 중요하다. 자신이 전달하고 싶은 메시지가 무엇인지, 그리고 그것을 어떻게 효과적으로 전달할 것인지가 발표자료의 핵심이라 생각한다.
질문의 글
질문의 글을 남길 때에도 타인의 입장을 고려하면서 글을 남기면 좋겠다. 블로그 댓글에 답변을 달다 보면 나도 모르게 가슴이 답답해지는 경우가 종종 있다. 본인만이 알 수 있는 것을 질문하는 경우, 글만으로는 무엇이 궁금한지 판단이 힘든 경우, 어디까지 설명해야 하는지 판단이 어려운 경우 등 난감한 경우가 많다. 타인은 나와 지식과 경험이 다르다는 것을 항상 유념하면서 최대한 구체적으로 글을 남기면 좋겠다.
이상으로, 그동안 블로그에 답글을 달면서 느꼈던 답답함을 글쓰기 방법이라는 미명 하에 풀어 보았습니다 ^^. 아래 2개는 글쓰기에 있어서 기타 소소한 팁입니다.
팁1. 두괄식의 사용
학술 논문이나 과학적 글을 쓸 때는 무조건 두괄식을 사용하는게 좋다. 두괄식은 각 단락의 첫 부분에 그 단락에서 하고자 하는 얘기를 한 문장으로 대표해서 적고, 이후 문장들에서 부연설명을 하는 방식이다. 예를 들어, 'A는 이렇다. B는 저렇다. 따라서, 제안 방법은 이러 저러하다' 방식 보다는 '제안 방법은 이렇다. 그 이유는 A는 이렇고 B는 저렇기 때문이다'와 같은 방식이 (독자 입장에서) 글의 흐름을 놓치지 않고 파악하는데 효과적이다. 이 역시 읽는 사람을 고려한 글쓰기이다. 단락 전체를 한 문장으로 정리하는게 쉽지는 않지만, 이런 연습을 통해 추상화 능력이 키워지고 자신이 무슨 얘기를 하고 싶어하는지 미리 생각을 정리하는 시간이 될 수 있다.
팁2. 간결한 글
짧게만 쓴다고 간결한 글은 아니다. 중요한 개념이나 강조하고 싶은 부분은 충분히 지면을 할애하는 것이 좋다. 다만, 한 두 문장으로 전달이 가능한 내용을 열 문장으로 늘여 쓰지만 않으면 된다. 간결한 글은 주제와 부합되면서 문장 하나 하나가 중복되지 않는 의미를 가지고 있는 글이다. 그리고 흥미로운 지식일지라도 글의 흐름에 큰 도움이 되지 않는 내용(사족)들은 과감히 제거하면 보다 좋은 글이 될 수 있다.
by 다크 프로그래머
'잡기장' 카테고리의 다른 글
| 디지털 피아노 건반소음 없애기 (8) | 2022.04.12 |
|---|---|
| 아래한글(hwp) 멈춤 현상과 파워포인트(ppt) (36) | 2018.12.22 |
| 기술의 가치 (7) | 2018.10.12 |
