원뿔곡선 이야기(원,타원,포물선,쌍곡선)
우리가 고등학교때 배우는 원, 타원, 포물선, 쌍곡선은 모두 conic section이라고 불리는 원뿔곡선 도형들이다.
원뿔곡선(Conic Section)
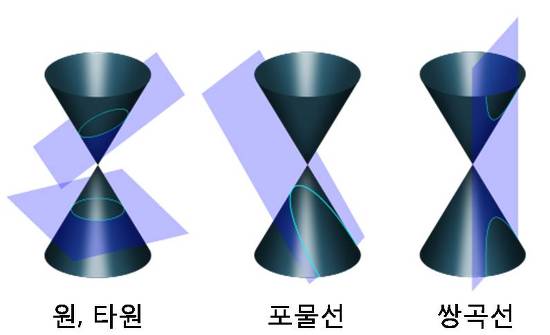
아이스크림 콘과 같은 원뿔 형태의 도형을 다양한 각도에서 잘 잘라보면 원, 타원, 포물선, 쌍곡선 단면을 얻을 수 있기 때문에 이들 도형을 conic section이라고 부르고 우리말로는 원뿔곡선이라 한다. section은 절단면을 의미한다.
<그림출처: Wikipedia>
콘의 밑면과 수평인 평면으로 자르면 원(circle)이 나오고, 이 평면을 조금 기울여서 자르면 타원(ellipse)이 나온다. 평면을 점점 세워가다보면 원뿔의 측면과 수평이 되는데 이 때의 단면이 포물선(parabola)이다. 그리고 여기서 평면을 더 세우면 쌍곡선(hyperbola)이 된다. 즉, 포물선은 타원과 쌍곡선의 경계에 있는 도형이다.
이심률(eccentricity)
이러한 원뿔곡선 도형들을 구분짓는 파라미터로 이심률(eccentricity)이 있다. 이심률은 원뿔곡선이 원에서 얼마나 동떨어졌느냐를 나타내는 값이다. 한자어로는 離心率 인데 중심에서 이탈한 정도, 또는 중심이 이탈한 정도를 나타내는 말로 풀이될 수 있을 것 같다.
어쨌든, 이심률은 e로 표현하는데 원의 이심률은 e = 0이고, 타원의 이심률은 0<e<1, 포물선의 이심률은 e = 1, 쌍곡선의 이심률은 e>1이다.
<그림출처: Wikipedia>
이심률의 계산은 e = (두 초점 사이의 거리)/(주축과 만나는 양 끝점 사이의 거리)로 계산할 수 있다. 원의 경우 중심(center)과 초점(focus)이 일치하므로 e = 0임을 알 수 있는데, 포물선은 왜 e = 1인 것일까?
초점(focus)
광학쪽에서 보면 초점은 빛이 모이는 점이다. 위 원뿔곡선들도 각각 초점을 가지고 있다. 원과 포물선은 초점이 하나이고 타원, 쌍곡선은 초점이 2개이다.
이러한 원뿔곡선들은 초점과 관련하여 재미있는 특성들을 가지고 있다.
포물선은 주축과 수평으로 들어온 빛들이 모두 초점으로 모이고, 타원은 한 초점에서 쏜 빛이 항상 다른 초점으로 모인다. 또한 쌍곡선은 어느 한 초점을 향해 들어온 빛들이 다른 하나의 초점으로 모인다.
이러한 원뿔곡선의 특징은 실생활에도 많이 활용된다.
전파망원경에 포물선의 원리가 이용된다는 것은 많이들 알고 있을 것이다. 전파원에서 들어오는 신호를 한 점으로 모으기 위해 전파망원경은 포물면을 이용한 접시형태의 반사체를 사용하고 초점 위치에 수신안테나를 설치한다. 반사체(접시)가 큰 경우에는 완벽한 포물면이 아닐 수 있기 때문에 초점 부근에 쌍곡선 면의 반사체를 설치하여 한번 더 신호를 모아준다고 한다.
KVN(한국우주전파관측망) - 그림출처: 한국천문연구원
또한 포물선 원리는 태양열 발전소에서 태양열을 한 점으로 모으기 위한 목적으로도 사용된다. 만일 포물면으로 된 거울을 만들어서 태양을 향하게 하면 돋보기처럼 초점 부근에서 발화가 일어날지도...
<스페인 PS10 태양열 발전소>
영국 런던의 세인트 폴 대성당(성 바오르 대성당)에 있는 속삭이는회랑(whispering gallery)에 가면 한쪽 복도에서 벽에 대고 속삭이면 건너편 복도에서 뚜렷이 잘 들린다고 한다. 이는 속삭이는회랑이 타원형의 둠 형태의 구조를 가지기 때문에 한쪽 초점에서 말한 소리가 사방에 펴졌다가 다른 초점에 모이기 때문이라고 한다.
그런데 타원이 아닌 구 중심에 서서 큰 소리를 내면 어떻게 될까?
원뿔곡선의 도형 방정식과 초점 구하기
원의 방정식은 알고 있지만 막상 도형이 방정식이 무슨 의미인지는 사람들이 잘 모르는 경우가 많다. 좌표계 공간에서 도형이란 어떤 조건을 만족시키는 점 (x, y)들의 집합을 의미하고 이걸 수식으로 나타낸 것이 도형의 방정식이다.
[원]
원은 한 점에서 같은 거리에 있는 점들의 자취(집합)이다. 따라서, 원의 중심을 (a, b), 중심에서의 거리를 r이라 하면 원은
을 만족시키는 점 (x, y)들의 집합이다.
[포물선]
포물선은 한 점과 한 직선에서 같은 거리에 있는 점들의 자취이다. 이 점이 앞서 말한 초점이 되고 직선은 준선이라고 부른다. 예를 들어, 초점이 (p, 0), 준선이 x = -p인 포물선의 방정식은
이며, 이를 정리하면
가 된다.
y = ax2+bx+c 또는 x = ay2+by+c가 포물선의 방정식임은 다 알 것이다. 그렇다면 이 포물선의 초점의 위치는 어디일까? 위 기본식을 이용하면 포물선 꼭지점으로부터 |1/(4a)| 떨어진 곳에 초점이 존재함을 알 수 있다.
[타원과 쌍곡선]
타원은 두 초점으로부터 거리의 합이 일정한 점들의 자취이고, 쌍곡선은 두 초점으로부터 거리의 차가 일정한 점들의 자취이다.
두 초점을 (-p,0), (p,0), 거리의 합을 2a라 하면 타원의 방정식은
가 되고, 이 식을 좀 복잡하긴 하지만 잘 정리해 보면
가 된다. 여기서 우리는 두 초점에서의 거리의 합이 바로 타원의 장축의 길이가 됨을 알 수 있다.
쌍곡선의 경우, 두 초점을 (-p,0), (p,0), 거리의 차를 2a라 하면 쌍곡선의 방정식은
가 되고, 마찬가지로 잘 정리해 보면
가 나온다.
by 다크 프로그래머