네 점을 지나는 구의 방정식
네 점을 지나는 구의 방정식은 어떻게 될까?
문득 생각해 본 문제입니다.
이걸 구해서 어디에 써먹을 수 있을지는 모르겠지만, 세 점을 지나는 원의 방정식을 구할 수 있다면 네 점을 지나는 구의 방정식도 구할 수 있지 않을까 하는 생각이 들었습니다.
일반적인 답이 있는지도 아직은 잘 모르겠지만 이걸 풀기 위한 과정 혹은 머리속의 사고의 흐름을 적어봅니다.
---------------
첫 번째 의문은 네 점이 주어지면 구가 유일하게 결정될까? 입니다.
원의 경우는 일직선상에 놓여있지 않은 세 점이 주어지면 원이 유일하게 결정됩니다.
구의 경우도 한 평면상에 있지 않은 네 점이 주어지면 구가 유일하게 결정될 것 같긴 합니다.
하지만, 머리속으로 3차원 공간에 점 4개를 찍어보고 생각해 보면 언뜻 이 점들을 모두 지나는 구가 잘 떠오르지 않습니다.
그래서 네 점을 가지고 삼각뿔을 그려봅니다.
네 점이 있으면 삼각뿔은 항상 그릴 수 있습니다.
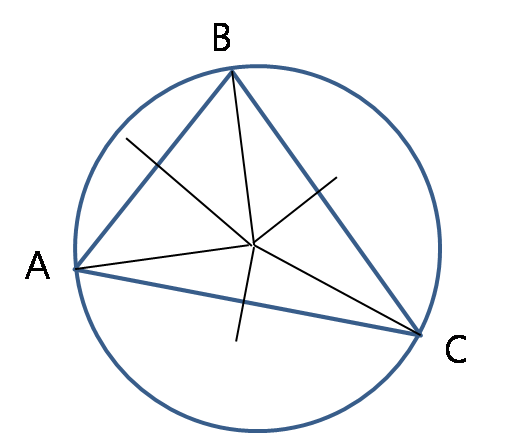
먼저, 점 ABC를 지나는 원을 그립니다.
이 원을 지나면서 점 D를 지나는 구를 생각해 봅니다. 이렇게 하면 구가 유일하게 결정되지 않을까요?
이렇게 해서 첫 번째 의문은 해결이 되었습니다.
---------------
두 번째 의문... 구의 중심은 어떻게 결정이 될까?
세 점을 지나는 원의 경우에 비추어 생각해 봅니다.
원의 경우는 세 현의 수직이등분선의 교점이 원의 중심입니다. 현이란, 직선과 원이 만나서 생기는 직선이 원에 의해 잘리는 부분입니다.
현을 구로 확장해 보면 평면과 구가 만나서 생기는 단면 즉, 원이 됩니다.
위 삼각뿔 그림에서 보면 삼각뿔은 4개의 면으로 이루어져 있기 때문에 각각의 면을 확장하여 총 4개의 평면을 생각할 수 있습니다.
그렇다면 이 4개의 평면이 구와 만나서 생기는 단면들의 중심을 지나면서 단면에 수직인 직선들이 만나는 점이 구의 중심이 된다는 말이 됩니다.
즉, 원 ABC의 중심축(세 점 ABC를 지나는 원의 중심을 지나면서 이 원에 수직인 직선), 원 ACD의 중심축, 원 ABD의 중심축, 원 BCD의 중심축이 서로 만나는 점이 구의 중심이라는 말이 됩니다.
그런데 정말 4개의 중심축들이 모두 한 점에서 만날까? 하는 의문이 듭니다. (3차원 공간에서는 직선 2개만 해도 서로 만나기가 무척 힘듭니다)
언뜻 위 삼각뿔 그림에서 생각해 보아도 과연 구의 중심에서 만날까 하는 의구심이 듭니다.
다시 세 점을 지나는 원의 경우에 비추어 생각해 봅니다.
원의 경우에서 현들의 수직이등분선들의 교점이 원의 중심인 이유는... 역으로 원의 중심에서 현에 수직인 선을 그어보면 항상 수직이등분선이 되고 이러한 수직이등분선은 항상 유일하기 때문입니다. 즉, 어떤 현의 수직이등분선이 2개가 존재할 수 없기 때문에 현의 수직이등분선은 원의 중심에서 현에 그린 수직이등분선과 동일하게 되므로 항상 원의 중심을 지나게 되고 이들의 교점이 원의 중심이 됩니다.
다시 구의 경우로 돌아가면, 구의 중심에서 현(여기서는 원)에 내린 수선은 항상 현의 중심축이 됩니다. 따라서, 마찬가지의 논리로 현들의 중심축은 모두 구의 중심을 지나게 되므로 이 중심축들의 교점을 구하면 구의 중심점을 구할 수 있게 됩니다.
여기서 다시 의문... 그런데 구의 중심을 구하기 위해 4개의 현의 중심축을 모두 사용할 필요가 있을까? 4 중심축이 모두 한 점에서 만난다면 아무거나 2개의 중심축의 교점만 구해도 되지 않을까? 입니다.
왠지 맞는 것 같습니다. 위 삼각뿔 그림에서 생각해 보면 아무 면이나 2개를 골라도 삼각뿔이 유일하게 결정됨을 알 수 있습니다.
여기까지 생각이 정리되고 보니 이제 저도 어떻게든 네 점을 지나는 구의 방정식을 구할 수는 있겠다는 확신이 생깁니다. 난이도를 떠나서 이제 남은건 단순한 계산과정 뿐입니다.
---------------(2013.6.22 추가)
이제 마지막 과정... 그런데 실제로 구의 중심 좌표를 어떻게 계산하지? 입니다.
네 점 A(x1,y1,z1), B(x2,y2,z2), C(x3,y3,z3), D(x4,y4,z4)에 대해 구의 중심 좌표를 일반적으로 구해 보는게 목적입니다.
여기서는 원 ABC의 중심축, 원 ABD의 중심축의 교점을 구해서 구의 중심을 구하도록 하겠습니다.
원 ABC의 중심을 O1, 원 ABD의 중심을 O2, 우리가 구하고자 하는 구의 중심을 M이라 하겠습니다.
일단 생각할 수 있는 가장 직접적인 방법은 두 중심축의 방정식을 구한 후 교점을 구하는 것입니다. 그런데, 그것보다는 벡터 M - O1이 평면 ABC와 수직이고 벡터 M - O2가 평면 ABD와 수직이라는 조건을 연립해서 M을 구하는 것이 좀더 효과적일 거라는 생각이 듭니다.
3D 공간에서 세 점에 의해 결정되는 평면에 수직인 벡터는 벡터의 외적을 이용하면 손쉽게 구할 수 있기 때문에, 원 ABC의 중심과 원 ABD의 중심을 구하는 것이 문제입니다.
즉, M - O1 = k1(A - O1)×(B - O1), M - O2 = k2(A - O2)×(B - O2)을 연립해서 상수 k1, k2를 구하면 M을 구할 수 있기 때문에 O1, O2만 구할 수 있으면 됩니다. (여기서 ×는 벡터의 외적을 나타냅니다)
그런데, 3D 공간에서 세 점을 지나는 원의 중심을 구하는 문제가 생각보다 만만치 않은 것 같습니다; 언뜻 좋은 생각이 떠오르지 않습니다..
그래서 2D에서 세 점을 지나는 원의 방정식을 구했던 과정을 다시 한번 돌이켜 보았습니다. (어떤 문제가 막혔을 때 이렇게 문제를 단순화시켜서 바라보면 의외로 쉽게 해결되는 경우가 많습니다. 매우 효과적인 문제 풀이법이며 제가 이 글에서 일관되게 사용하고 있는 방법이기도 합니다)
(2013.6.23 추가)
2D의 경우에서는 위 그림과 같이 각 변의 수직 이등분선의 교점을 구해서 원의 중심을 구했었습니다. 그런데, 이걸 3D로 확장해 보면 각 변의 중점을 지나면서 각 변에 수직인 평면들의 교선이 됩니다. 즉, 원래 구하고자 했던 원 ABC의 중심축이 됨을 알 수 있습니다.
어라?
그렇다면 굳이 힘들게 원 ABC의 중점을 구할 필요 없이 교선을 구함으로써 원 ABC의 중심축을 구할 수 있게 되었습니다. 이제 원 ABC의 중심축과 원 ABD의 중심축만 연립하면 구의 중점이 나옵니다.
이제야 깨닫게 된 것이지만.. 훨씬 쉬운 길이 있었는데, 제가 먼 길을 돌아서 온 것 같습니다.
처음의 삼각뿔 ABCD 그림으로 다시 되돌아가 생각해 보면, 삼각뿔 ABCD는 AB, AC, AD, BC, BC, DC 총 6개의 변으로 이루어져 있는데, 각 변의 수직 이등분 평면이 모두 구의 중점을 지남을 알 수 있습니다. 따라서, 한 평면 위에 있지 않은 임의의 3개의 변을 뽑아서 수직 이등분 평면들을 연립하면 구의 중심을 구할 수 있음을 알 수 있습니다.
여기서는 AB, BC, AD의 수직 이등분 평면을 연립하여 구의 중심을 구하도록 하겠습니다.
네 점의 좌표가 A(x1,y1,z1), B(x2,y2,z2), C(x3,y3,z3), D(x4,y4,z4)일 때, 선분 AB의 수직 이등분 평면 방정식은 다음과 같습니다.
※ 점 p = (a, b, c)를 지나면서 h = (h1, h2, h3)를 법선 벡터로 하는 평면의 방정식은 h·(x-p)=0 즉, h1(x-a) + h2(y-b) + h3(z-c) = 0 임을 상기하시기 바랍니다.
위 평면 방정식을 다시 쓰면 아래와 같이 정리할 수 있습니다.
마찬가지로, 선분 BC의 수직 이등분 평면 방정식과 선분 AD의 수직 이등분 평면 방정식도 다음과 같습니다.
이제 위 식들을 행렬식으로 표현하여 연립하도록 하겠습니다. 그러면 구의 중심 (x, y, z)는 다음과 같이 계산됩니다.
인터넷을 검색해 보면 3 x 3 역행렬을 구하는 식은 쉽게 찾을 수 있을 것입니다.
이상으로 네 점을 지나는 구의 중심을 일반적으로 구할 수 있었습니다. 구의 중점만 알면 구의 반지름은 쉽게 계산이 되므로, 네 점을 지나는 구의 방정식이 결정된 셈입니다 ◇
☞ 위 글은 미리 문제를 풀어놓고 생각을 정리하여 글로 쓴 글이 아니라 먼저 글쓰기를 시작한 후에 실제 과정을 그때 그때 글로 옮긴 글입니다.
☞ 위에서 구한 식이 정말 맞는지 아직 검산은 하지 못했습니다. 아마 맞을 거라 생각하지만 혹시 모르니 나중에라도 한번은 검산을 해 봐야겠네요.
by 다크 프로그래머